|
앞선 포스트에서 파형률과 파고율을 구하는 공식을 암기해 보았는데요, 공식만 알면 뭐하겠습니까? 각 파형별 실효값과 평균값을 모르면 답을 구할 수 없겠죠.
그래서 이번 포스팅에서는 각 파형별 실효값과 평균값을 이미지맵을 통해 암기해 봅니다.
요즘은 한글 맞춤법에 따라 실효값을 '실횻값'으로, 최대값을 '최댓값'으로 표기를 하는 것 같네요. 발음상의 차이일 뿐, 전기기사 시험이 '우리말 겨루기' 시험은 아니기에 여기서는 기존대로 실효값, 최대값으로 표기를 하겠습니다. :)
〓
아래의 표는 전기기사 수험서나 인터넷을 좀 뒤져보면 많이 볼 수 있는 파형별 최대값, 실효값, 평균값 테이블입니다. 이 표 하나 딸랑 던져주고 무조건 암기하라고 합니다. ㅎㅎ 정신적 고문이 따로 없습니다. 교류의 기본인 정현파 이외에도 반파, 삼각파, 구형파, 구형 반파 등 무슨 조폭 '○○파'도 아니고... 이 표 무작정 외워봤자 얼마 못 가 다 까먹고요 헷갈리기 마련입니다.
수학적 증명이나 유도 등을 통해서 각 숫자들이 나온 이유는 다 있을 것입니다.
하지만 기사 시험의 수준에서 각 숫자들이 나온 과정까지는 알 필요가 없습니다. 우리는 결과값을 가지고 파형률, 파고율 공식에 넣어 답을 구하면 그만이니까요.
그나마 구형파는 모두 값이 '1'이라 불행 중 다행인가 싶습니다. :)
최대값 '1'을 기준으로, 각 파형별 실효값과 평균값을 단순 암기가 아닌, 제가 만든 이미지맵 [그:리다]를 통한 연상법으로 쉽게 암기를 해 봅니다.
〓
먼저, 교류의 기본파형인 '정현파(전파)'를 보겠습니다.
정현파의 실효값은 '1÷√2' 입니다.
실효값의 '효'에서 숨겨진 숫자를 한번 찾아볼까요?
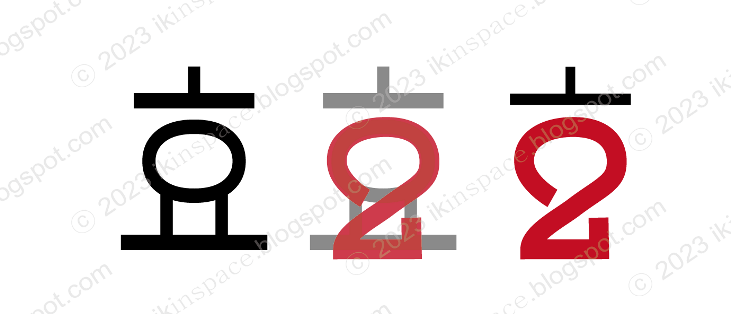
아래 그림을 보면, '효' 안의 '요' 부분을 숫자 '2'로 바꿀 수 있습니다.
실눈 감고 가만히 보면, '요'가 숫자 '2'로 보입니다. :)
또한, '효'의 맨 위에 있는 'ㅗ' 역시 숫자 '1'과 분수식의 '―'로 바꿀 수 있습니다. 분자에 숫자 '1' 있는 것 보이시나요?
그리고 '실효값'의 '실'.. '실'의 아랫받침 'ㄹ'을 정현파의 ∩∪파형처럼 휘갈겨쓰면 전체적으로 아래와 같은 이미지가 됩니다.
휘갈겨 쓴 'ㄹ'은 '√'(루트) 모양이 되고요, 그게 이어져 '효'의 '요'자 위로 지나갑니다.
'효'의 '요'는 숫자 '2', 'ㅗ'의 '│'은 숫자 '1'이 되어, 전체적으로 보면, '1÷√2'의 이미지가 만들어 집니다. 숫자를 무작정 암기하는게 아니라 위의 '실효' 이미지를 머릿속에 사진 찍듯이 통째로 기억합니다.
〓
정현파의 평균값은 '2÷π' 입니다.
평균값의 '평'이라는 글자를 통해 '뭔가 평평한 것(?)'을 떠 올립니다.
바로 선반이나 도마처럼 생긴 'π'(파이) 입니다.
아래 그림처럼, 평평한 'π' 위에 긴 막대기를 하나 놓고 가운데를 힘껏 내려쳐(평균을 낸다는 뜻) 두 동강이 내는 이미지를 상상합니다. 막대기가 두 동강 나서 2개가 되었습니다.
'π' 위에서 두(2) 동강 난 막대기..
이 이미지맵을 통해 '2÷π'를 유추하여 암기할 수 있습니다.
〓
여기에 바로 이어서, 반파 정현파의 실효값과 평균값까지 암기해 봅니다.
위의 정현파의 실효값, 평균값 이미지맵만 기억하고 있으면 따로 암기할 필요가 없습니다.
반파라는 것은, 단순히 뜻만 놓고 보면 '전파의 절반'이라는 뜻이죠.
그래서 정현파의 실효값, 평균값 이미지맵을 아래 그림처럼 각각 절반으로 나누어 봅니다.
'평균값' 이미지맵을 절반으로 나누었더니, 분자의 두 동강난 막대기는 한(1)개 만 남았고, 밑의 'π'(파이)는 숫자가 아니기에 절반만 남았음에도 그대로 'π'(파이) 입니다. 그래서 '1÷π' 입니다.
이처럼 정현파의 실효값, 평균값 이미지맵만 기억하면, 반파까지 유추하여 암기할 수 있습니다. :)
〓
삼각파(톱니파, △△△)의 경우를 봅니다.
삼각파의 실효값은 '1÷√3'이고, 평균값은 '1÷2'입니다.
'삼각, 톱니'하면 뭔가 뾰족하고 날카로운 이미지가 떠오릅니다.
그래서 실효값의 '실', 평균값의 '평'을 아래와 같은 이미지맵으로 표현해 보았습니다.
'실'의 'ㅅ'은 '√'(루트) 모양으로, 아랫받침 'ㄹ'은 숫자 '3'으로 뾰족하게 표현하였습니다. 모음 'ㅣ'는 숫자 '1'과 모양이 같죠.
그래서 전체적인 모양을 보면 분모에 '√3'이, 분자에 '1'이 있는 이미지입니다.
따라서 실효값의 '실'을 톱니 같은 뾰족한 이미지맵으로 바꾸어 '√3분의 1'을 유추하여 암기할 수 있어요.
'평균값'의 '평'에서 'ㅍ'은 뾰족한 드라큘라 송곳니로 표현하였습니다. 송곳니가 2개니까 숫자 '2'이고요, 'ㅕ'의 'ㅣ' 역시 숫자 '1'과 생김새가 비슷합니다. 그래서 전체적인 모양을 보면 순서대로 숫자 '2'와 숫자 '1'이 되어 '2분의 1'을 암기할 수 있습니다. :)
〓
마지막, 구형 반파입니다.
구형파의 경우 최대값, 실효값, 평균값이 모두 1이라서 암기하는데 크게 지장이 없는 반면, 구형 반파는 실효값이 '1÷√2', 평균값이 '1÷2' 입니다.
이 역시도 단순암기보다는 그림을 이용해 이해(?)하면서 암기를 해 보겠습니다.
구형파는 네모 반듯한 모양입니다. 예를 들어 '정사각형'이라고 해보죠.
'구형 반파'는 '구형파의 반'이라는 뜻이므로 ★정사각형을 반으로 나누어★ 보겠습니다.
단, 실효값과 평균값의 나누는 방법이 각각 다릅니다.
아래 그림처럼 실효값은 '대각선'으로 나누고, 평균값은 '가로'로 나눕니다.
실효값의 자음 'ㅅ'을 정사각형의 구석에 위치시키면 대각선으로 자를 수 있겠죠?
그리고, 평균값은 말그대로 '평평하게' 가로로 자릅니다.
그러면 아래와 같은 모습이 되는데요..
먼저 실효값의 경우, 정사각형의 대각선 비율비는 '1:√2' 입니다. 그리고 평균값의 비율비는 '가로:세로=1:0.5=2:1'이 됩니다.
정리하면,
구형파의 정사각형을 실효값은 대각선으로, 평균값은 가로로 반토막(반파) 내었을 때, 남은 조각의 비율비를 각각 유추하여 '1÷√2', '1÷2'을 암기할 수 있습니다.
숫자를 암기하는 것이 아니라, 그림(이미지)을 기억하는 겁니다. :)
〓
기출문제를 보겠습니다.
[문제1] 파형이 톱니파인 경우 파형률은 약 얼마인가?
1) 1.155
2) 1.732
3) 1.414
4) 0.577
정답은 1번.
[문제2] 순시치 전류 i(t)=Imㆍsin(ωt+θ) A의 파고율은 얼마인가?
1) 0.577
2) 0.707
3) 1.414
4) 1.732
정답은 3번.
⚠
본 콘텐츠의 저작권은 「꿈:틀, In Space」에 있습니다.
아이디어 도용, 무단복제와 인용을 금합니다.









No comments:
Post a Comment